|
EMPIRE DA
v1.9.1
Data assimilation codes using EMPIRE communication
|
|
EMPIRE DA
v1.9.1
Data assimilation codes using EMPIRE communication
|
Author: PA Browne. Time-stamp: <2016-01-16 00:54:55 pbrowne>
\(\frac{\mathrm{d}x_k}{\mathrm{d}t} = -x_{k-2}x_{k-1} + x_{k-1}x_{x+1} - x_k + F\)
Fortunately, there is a model already within EMPIRE that can do all this. Build it with the command
Now you can check that a model executable was created. It will be found in the binaries folder bin/
Before any data assimilation can be done with the model, we must specify operators such as the observation operator H, its error covariance R, and a few others. Below, we list how we shall set these up in the file model_specific.f90, which is located in the top directory of EMPIRE.
We shall have an observation network that does not change with time. We are going to observe every other grid point directly.
That is, \( y = H(x) = \begin{bmatrix} x_1 \\ x_3 \\ x_5 \\ \vdots \\ x_{N-1} \end{bmatrix} \).
Note that here we are using Fortran indexing (starting from 1). For simplicity, we will assume that \(N\) is odd. Hence the observation operator should look as follows.
\(H\) is therefore a matrix in \(\mathbb{R}^{\frac{N}{2}\times N}\) such that
\(H = \begin{bmatrix} 1 & 0 &0 &0 & 0 & 0 &0 & \cdots & 0 &0 \\ 0 & 0 &1 &0 & 0 & 0 &0 & \cdots & 0 &0 \\ 0 & 0 &0 &0 & 1 & 0 &0 & \cdots & 0 &0 \\ \vdots & \vdots &\vdots &\vdots & \vdots & \vdots &\ddots & \cdots & \vdots &\vdots \\ 0 & 0 &0 &0 & 0 & 0 &0 & \cdots & 1 &0 \end{bmatrix}\)
We never form this matrix, instead we simply implement H (and its transpose, HT) by selecting (inserting) the appropriate values from (to) the state vector. Note that we have to do this for an arbitrary number of state vectors.
Similarly, for the transpose of this observation operator, we can write this as follows:
Let us assume that we have homogeneous, uncorrelated observation errors such that \(R = \sigma^2I\). For this example, \(\sigma^2=0.1\). Then we can code multiplication by R in the following way:
Similarly, application of \(R^\frac{1}{2}\) can be done as:
We also need to have the application of \(R^{-1}\) and \(R^{-\frac{1}{2}}\). These can be done with the following subroutines:
To make an initial ensemble, we can use a background error covariance matrix, \(B\). In this example, \(B = 0.2I\). There are two functions of this matrix that we could need: \(B^{\frac{1}{2}}\) and \(B^{-1}\). These can be coded in the following ways:
If \(i\) and \(j\) are two different grid points, then we define the correlation, \(C_{ij}\) between the model error at grid points \(x_i\) and \(x_j\) to be
\( C_{ij} =\begin{cases} 1 & \text{if } i=j\\ \frac{2}{3} & \text{if } |i-j|=1 \\ \frac{1}{6} & \text{if } |i-j|=2 \\ 0 & \text{otherwise} \end{cases}\)
Then, we define the model error covariance matrix \(Q = \alpha^2 \frac{3}{2} C\). Hence
\(Q^{\frac{1}{2}} = \alpha\begin{bmatrix} 1 & 0.5 & 0 & 0 & \cdots & 0 & 0.5 \\ 0.5 & 1 & 0.5 & 0 & \cdots & 0 & 0 \\ 0 & 0.5 & 1 & 0.5 & \cdots & 0 & 0 \\ \vdots & \vdots & \ddots & \ddots & \ddots & \vdots & \vdots \\ 0 & 0 & 0 & 0 & \cdots & 1 & 0.5 \\ 0.5 & 0 & 0 & 0 & \cdots & 0.5 & 1 \\ \end{bmatrix}\)
Thus this can be coded as:
For simplicity, we shall leave the operator Q as the default one. This will simply apply Qhalf twice in order to apply the Q operator.
For the LETKF, we have to be able to do localisation. To do so, we define a distance measure between the observations and the grid points.
The model is cyclic, so we can say that all the variables lie in the interval [0,1]. To find the position of variable \(x_{xp}\) we can therefore divide \(xp\) by the total number of gridpoints. To find the position of observation \(y_{yp}\), we note that \(y\) corresponds to every other gridpoint of \(x\). Hence its position in the interval [0,1] can be calculated as \(2yp-1\) divided by the total number of gridpoints. The distance between these two positions is then either the distance directly within the interval [0,1], or the distance wrapping around this interval. The code implementing this is below:
Here we tell EMPIRE how large the model is, how many observations we have per observation time. In this experiment we are going to have observations at a fixed frequency. The total number of observations in time, and the frequency of observations will be read in at run time to the variables pf%time_obs and pf%time_bwn_obs, respectively. Here we also call timestep_data_set_total to tell EMPIRE how long the model run will be. The "sanity check" below has helped me countless times when debugging - it serves no other purpose than to help identify errors.
In this example, the observational network is not going to change through time. Reconfigure model is called after each analysis is performed, so that the observational network can be reconfigured for the next set of observations. As the observation is going to be at the same time interval as for the last one, and the operators H and R remain constant, we this subroutine can be left blank as below. Note it cannot be removed as this will lead to a compilation error.
We are now at a point where we can compile the code. Go to the same directory as model_specific.f90 and simply type the command
Now you can check that a new empire executable was created. It will be found in the binaries folder bin/, run the following command and ensure that it has an up-to-date timestamp:
Now that we have both the model and EMPIRE compiled, we are in a position to execute the codes and therefore do some experiments. We shall do a twin experiment, where we first run the model to act as a "truth" and from which we generate observations. Then afterwards we will run an ensemble from different starting conditions and attempt to use the observations we have taken to stay close to the truth.
The first step is to run the truth and generate the observations.
We have to define the runtime parameters that EMPIRE requires. These are found in the file empire.nml.
In empire.nml, the namelist should appear as follows:
Now let us move to an appropriate folder to run:
In this folder, you must have the empire.nml file located. Check this with an ls command.
The model also needs a driving file. It needs to be called l96.nml, which is a standard Fortran namelist file. To set the parameters for the run we shall do, the l96.nml should look as follows:
Now we want to run a single ensemble member. For this model, each ensemble member uses a single MPI process. So we must launch a total of 1 MPI processes to run the model. To output the truth, we only need a single EMPIRE process. The mpirun syntax for doing this is as follows:
Now after the code has finished (a matter of seconds), let us look for some output. Check to see the observation files have been created:
There should only be one: obs_000001. This is going to be the observation file that we use in later.
Before we do the assimilation, let's get something to compare with. The comparison that we can do is against a model run where we have not done any assimilation.
We want EMPIRE to run for the same number of timesteps as before, so in empire.nml we set time_obs and time_bwn_obs as we had previously. We also want to create the initial ensemble in the same way, so init remains 'B'. We are no longer generating the data, so remove gen_data to use its default value false. Lastly, we have to tell EMPIRE to propagate the ensemble members forward stochastically without assimilating the observations. We do this by setting the filter type filter to 'SE' (Stochastic Ensemble).
In empire.nml, the namelist should appear as follows:
Now we want to execute this but using more than one ensemble member. 32 ensemble members seems like a good number. As we have more than 1 ensemble member, we can use more than one EMPIRE process. Here we will use 4, and therefore each EMPIRE process will be dealing with 8 ensemble members.
We run this with the mpirun command:
All that is necessary to do in order to run an assimilation is now to change filter to correspond to the method we want to use. Let us use the LETKF (as we spent so long ensuring the distance calculation for it earlier).
Hence modify filter in empire.nml to 'LE' so that the namelist appears as:
Run this the same way as you ran the stochastic ensemble with the mpirun command:
For this we shall use python, with numpy and matplotlib
The python script examples/lorenz96/tutorial_lorenz96_plot.py is able to produce some plots of trajectories from the output. Run this with the command
If all has gone to plan, you should see a plot looking like the one below:
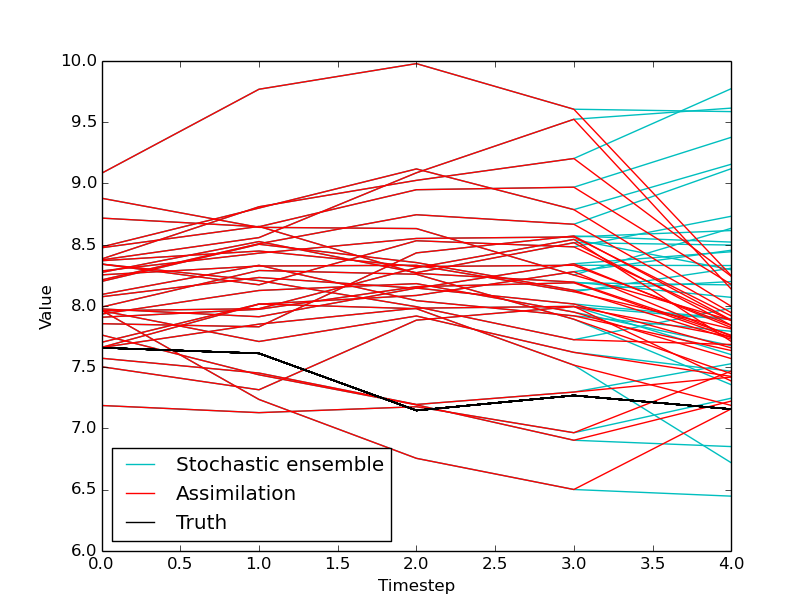
These can be found in the file examples/lorenz96/tutorial_lorenz96_script.sh