4denvar_fcn.f90 File Reference

Go to the source code of this file.

Functions/Subroutines
subroutine	fcn (n, x, f, g)
	This is the subroutine which the optimization routines call to get the objective function value and its gradient. More...
subroutine	fourdenvar_fcn (n, v, f, g)
	subroutine to provide the objective function and gradient for 4dEnVar. More...
subroutine	convert_control_to_state (n, v, stateDim, x)
	a subroutine to convert the optimization control variable to a model state vector More...
subroutine	fourdenvar_fcn_master (n, v, f, g, leave)
subroutine	fourdenvar_fcn_slave (n, v, leave)

Function/Subroutine Documentation

subroutine convert_control_to_state	(	integer, intent(in)	n,
		real(kind=rk), dimension(n), intent(in)	v,
		integer, intent(in)	stateDim,
		real(kind=rk), dimension(statedim), intent(out)	x
	)

a subroutine to convert the optimization control variable to a model state vector

this must be called by all processes on pf_mpi_comm

and the result x is known to all processes

Parameters

[in]	n	the dimension of the control variable
[in]	v	the optimization control variable
[in]	statedim	the dimension of the model state
[out]	x	the resulting model state

Definition at line 153 of file 4denvar_fcn.f90.

Here is the caller graph for this function:

subroutine fcn	(	integer, intent(in)	n,
		real(kind=kind(1.0d0)), dimension(n), intent(in)	x,
		real(kind=kind(1.0d0)), intent(out)	f,
		real(kind=kind(1.0d0)), dimension(n), intent(out)	g
	)

This is the subroutine which the optimization routines call to get the objective function value and its gradient.

Parameters

[in]	n	the dimension of the optimzation problem
[in]	x	the current optimization state
[out]	f	the objective function value
[out]	g	the gradient of the objective function

Definition at line 31 of file 4denvar_fcn.f90.

Here is the call graph for this function:

Here is the caller graph for this function:

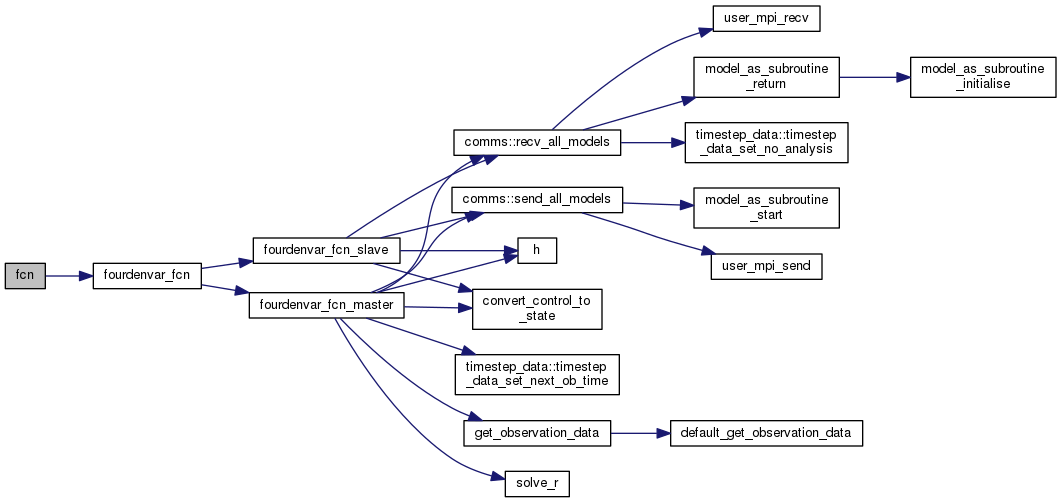
subroutine fourdenvar_fcn	(	integer, intent(in)	n,
		real(kind=rk), dimension(n), intent(in)	v,
		real(kind=rk), intent(out)	f,
		real(kind=kind(1.0d0)), dimension(n), intent(out)	g
	)

subroutine to provide the objective function and gradient for 4dEnVar.

Let \(x\) be the state we wish to find using Var.

Then we define \(X_k := \{ x_1(k)-x(k);\ldots;x_m(k)-x(k)\}\)

to be the ensemble perturbation matrix,

where \(x_j(k)\) is the jth ensemble member at time \(k\)

and \(x(k)\) is the optimization solution integrated forward in time to timestep \(k\).

The objective function considered is

\(J(x) = \frac{1}{2}(x-x_b)^TB^{-1}(x-x_b) + \frac{1}{2}\sum_i(y_i-H_i(M_i(x)))^T R_i^{-1} (y_i - H_i(M_i(x)) )\)

where \(x_b\) is a background guess, \(B\) the background error covariance matrix,

\(y_i\) observations at a timestep \(i\), \(H_i\) the corresponding observation operator with associated observation error covariance matrix \(R_i\) and \(M_i\) the model which propogates a state from time \(0\) to the observation timestep \(i\).

In this code, \(B:= \frac{1}{m-1}X_0X_0^T\).

We make the following control variable transform:

\(x = X_0 v + x_b\) where \(v \in \mathbb{R}^m\).

Then the objective function can be re-written as a function of v,

\(f=J(x)=J(v) = \frac{1}{2}(m-1)v^Tv + \frac{1}{2}\sum_i(y_i-H_i(M_i(X_0v+x_b)))^T R_i^{-1} (y_i - H_i(M_i(X_0v+x_b)) )\).

The gradient of the objective function can then be written

\(g = \nabla_vJ(v) \approx (m-1)v - \sum_i (H_i(X_i))^T R_i^{-1} (y_i - H_i(M_i(X_0v+x_b)) \)

which is exact if \(H_i\) and \(M_i\) are linear and \(X_0\) is invertible (at least I assume there has to be this condition on \(X_0\)...).

Note this is not exactly the 4dEnVar algorithm as given by Liu, Xian and Wang (2008) as the ensemble perturbation matrix here are perturbations around the current var solution, not the perturbations around \(M_i(x_b)\). i.e. \(X_i = X_i(x)=X_i(v)\).

Parameters

[in]	n	this is the dimension of the optimization control variable, so the number of ensemble members-1
[in]	v	this is the optimization control variable
[out]	f	the 4dvar objective function
[out]	g	the gradient of the 4dvar objective function

Definition at line 105 of file 4denvar_fcn.f90.

Here is the call graph for this function:

Here is the caller graph for this function:

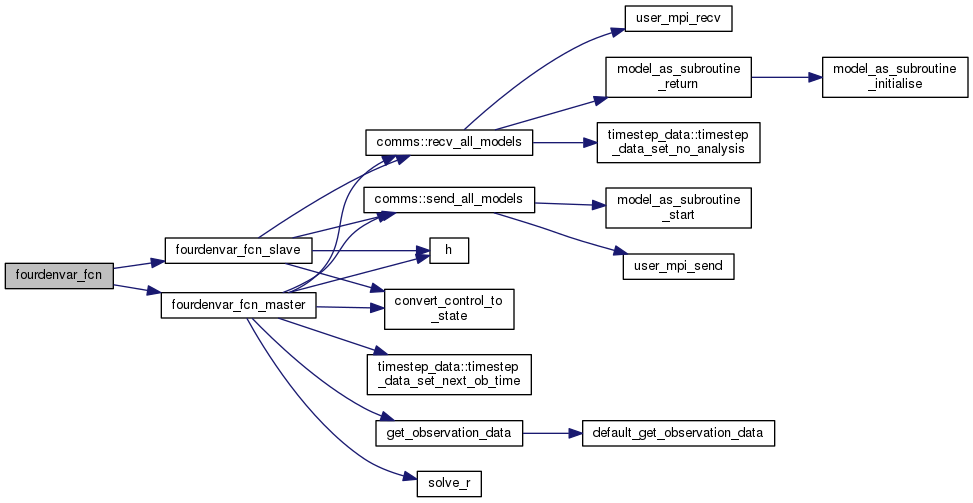
subroutine fourdenvar_fcn_master	(	integer, intent(in)	n,
		real(kind=rk), dimension(n), intent(in)	v,
		real(kind=rk), intent(out)	f,
		real(kind=kind(1.0d0)), dimension(n), intent(out)	g,
		logical, intent(out)	leave
	)

Parameters

[in]	n	this is the dimension of the optimization control variable, so the number of ensemble members-1
[in]	v	this is the optimization control variable
[out]	f	the 4dvar objective function
[out]	g	the gradient of the 4dvar objective function

Definition at line 198 of file 4denvar_fcn.f90.

Here is the call graph for this function:

Here is the caller graph for this function:

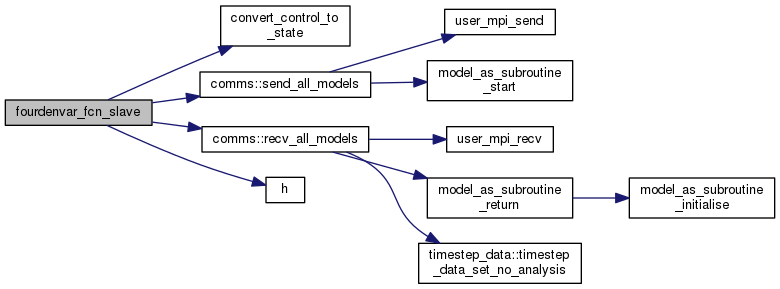
subroutine fourdenvar_fcn_slave	(	integer, intent(in)	n,
		real(kind=rk), dimension(n), intent(in)	v,
		logical, intent(out)	leave
	)

Parameters

[in]	n	this is the dimension of the optimization control variable, so the number of ensemble members-1
[in]	v	this is the optimization control variable

Definition at line 404 of file 4denvar_fcn.f90.

Here is the call graph for this function:

Here is the caller graph for this function: